| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- SQLP
- database
- RAC
- 결합인덱스구조
- 데이터모델링
- 로버트C마틴
- B*Tree
- 친절한SQL튜닝
- leetcode215
- join
- Oracle
- db
- B*Tree인덱스구조
- B*Tree인덱스
- 리트코드215
- clean code
- 알고리즘
- SQL튜닝의시작
- intellij
- SQLD
- 파이썬
- 오라클튜닝
- 리눅스
- index fast full scan
- 오라클
- 조인
- table full scan
- 클린 코드
- 클린코드
- heapq
- Today
- Total
개발노트
[자료구조] 힙(heap) - 파이썬 python 본문
우선순위 큐란?
우선순위 큐는 먼저 들어온 데이터가 먼저 처리되는 일반적인 큐와 달리, 우선순위가 높은 데이터부터 처리되는 자료구조이다. 배열, 연결리스트, 힙(Heap)으로 모두 구현할 수 있지만 일반적으로는 시간복잡도가 적은 힙(Heap)을 사용한다.
힙(Heap)
- 힙(heap)은 힙의 특성(최소 힙에서는 부모가 항상 자식보다 작거나 같다)을 만족하는 거의 완전한 트리인 특수한 트리 기반의 자료구조이다.
- 최솟값, 최댓값을 찾아내는 연산을 빠르게 할 때 사용한다.
- 힙은 최소 힙(Min Heap)과 최대 힙(Max Heap)으로 구분할 수 있다.
- 힙은 정렬된 구조가 아니다. 부모-자식 간의 관계만 정의할 뿐, 좌우에 대한 관계는 정의하지 않는다.
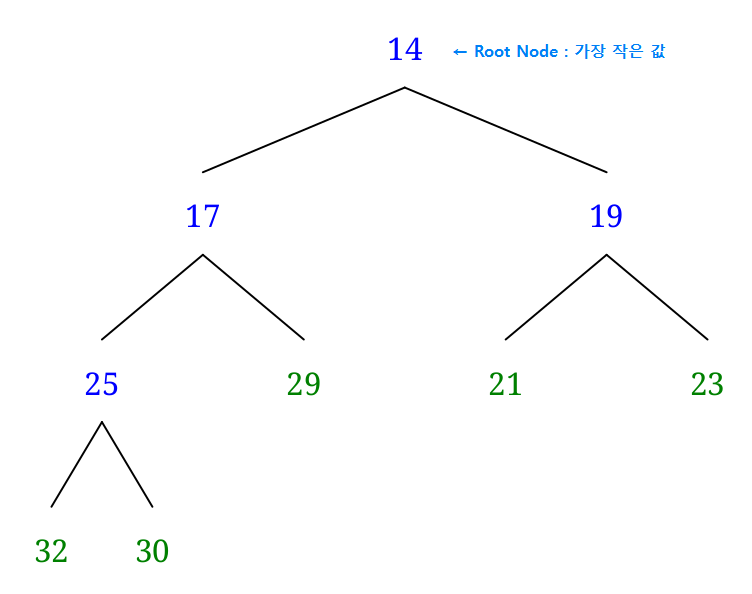
- 최소 힙: 루트노드가 가장 작은 값을 가지며, 항상 부모노드는 자식노드보다 작은 값을 가짐
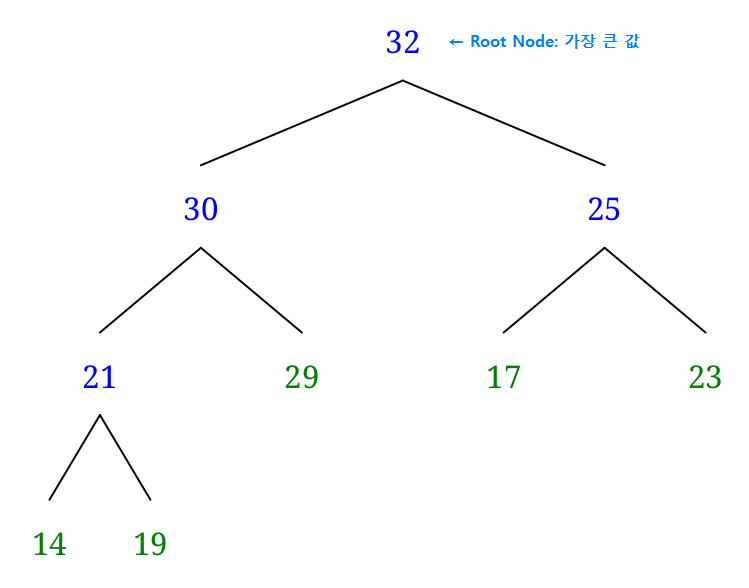
- 최대 힙: 루트노드가 가장 큰 값을 가지며, 항상 부모노드는 자식노드보다 큰 값을 가짐
- 최대 이진 힙의 배열 표현
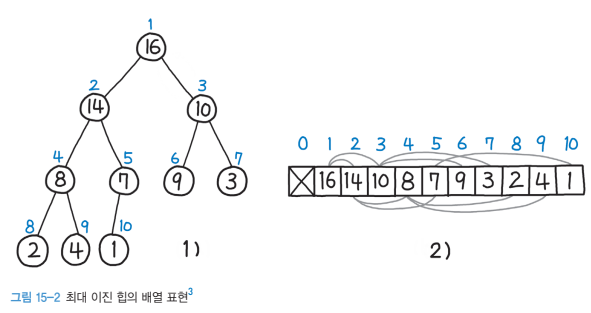
완전 이진 트리 형태인 이진 힙은 배열에 빈틈없이 배치가 가능하며, 대개 트리의 배열 표현의 경우 계산을 편하게 하기 위해 인덱스는 1부터 사용한다.
파이썬 구현
파이썬에서는 우선순위 큐를 구현할 때 2가지 방법을 이용할 수 있다.
바로 PriorityQueue 와 heapq 이다.
코딩테스트에서는 heapq 가 PriorityQueue 보다 실행시간이 적어 일반적으로 더 많이 사용된다.
🍯꿀팁🍯
heapq 와 PriorityQueue 모두 최소힙을 다루기 때문에, 최대힙 사용이 필요할 때는 마이너스(-) 부호로 바꿔서 값 push 하여 사용한다.
PriorityQueue
- 우선순위 큐 클래스이다. 사용할 때는 클래스를 import 한 뒤 변수에 객체를 생성해서 사용한다.
- put, get
- 최소힙
from queue import PriorityQueue
print('------ MIN HEAP ------')
pq = PriorityQueue()
pq.put(1)
pq.put(10)
pq.put(11)
pq.put(5)
pq.put(6)
print(pq.get())
print(pq.get())
print(pq.get())
print(pq.get())
print(pq.get())
print('------ MAX HEAP ------')
pq = PriorityQueue()
pq.put(-1)
pq.put(-10)
pq.put(-11)
pq.put(-5)
pq.put(-6)
print(-pq.get())
print(-pq.get())
print(-pq.get())
print(-pq.get())
print(-pq.get())heapq 사용하기
- 우선순위 큐 모듈로, 객체 생성 없이 바로 메서드를 사용한다.
- heappush, heappop, heapify
- 최소힙
- O(logN) 의 시간복잡도를 갖는다.
import heapq
print('------ MIN HEAP ------')
pq = []
heapq.heappush(pq,1)
heapq.heappush(pq,10)
heapq.heappush(pq,11)
heapq.heappush(pq,5)
heapq.heappush(pq,3)
print(heapq.heappop(pq))
print(heapq.heappop(pq))
print(heapq.heappop(pq))
print(heapq.heappop(pq))
print(heapq.heappop(pq))
print('------ MAX HEAP ------')
pq = []
heapq.heappush(pq,-1)
heapq.heappush(pq,-10)
heapq.heappush(pq,-11)
heapq.heappush(pq,-5)
heapq.heappush(pq,-3)
print(-heapq.heappop(pq))
print(-heapq.heappop(pq))
print(-heapq.heappop(pq))
print(-heapq.heappop(pq))
print(-heapq.heappop(pq))
heapq 의 heappush, heappop 구현하기
class BinaryHeap(object):
def __init__(self):
self.items = [None] # 0번 인덱스는 none 으로 할당하여 1부터 사용하게 함// 이유? 인덱스 계산을 깔끔하게 하려고
def __len__(self):
return len(self.items) - 1
# 삽입시 싱행, 반복 구조 구현
def _percolate_up(self):
i = len(self) # 자식노드는 현재 배열의 길이를 인덱스로 갖는다.
parent = i//2 # 부모노드의 인덱스는 자식노드의 2로 나눈 몫이다.
# i 가 1이 될때까지 진행
while parent > 0:
# 부모가 자식보다 크다면 item 변경
if self.items[i] < self.items[parent]:
self.items[parent], self.items[i] = self.items[i], self.items[parent]
else:
break # swap 이 필요없다면 더이상 진행안해도 되기 때문에 반복문 빠져나감
## 부모 인덱스가 자식인덱스가 됨
i = parent
parent = i//2
# 파이썬 모듈의 heapq.heappush()
def insert(self, k):
## 배열에 새로운 값 k 추가
self.items.append(k)
## min heap 수행
self._percolate_up()
# 추출 시 실행, 재귀 구조 구현
def _percolate_down(self, idx):
## idx 의 자식 인덱스 계산
left = idx*2
right = idx*2+1
smallest = idx
## 1) 왼쪽 자식이 부모보다 작을 때
if left <= len(self) and self.items[left] < self.items[smallest]:
smallest = left
## 2) 오른쪽 자식이 부모보다 작을 때
if right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right
## 1), 2) 를 통해 부모 인덱스가 자식과 swap 되었을 때 아이템도 변경
if smallest != idx:
self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
## swap 되었으니 다음 자식들과 또 비교(재귀)
self._percolate_down(smallest)
# 파이썬 모듈의 heapq.heappop()
def extract(self):
extracted = self.items[1] ## root node 추출 -> 이 값이 return 값!! (O(1))
## root node 추출 후 다시 완전 이진 트리 구조로 수정
self.items[1] = self.items[len(self)] ## 가장 마지막 요소 인덱스 가져와서 root node 에 위치
self.items.pop() ## 마지막 요소를 root 로 옮겼으니 pop 해서 제거
self._percolate_down(1)
return extracted
heapArr = BinaryHeap()
heapArr.insert(100)
heapArr.insert(1)
heapArr.insert(43)
heapArr.insert(3)
heapArr.insert(2)
print(len(heapArr)) # 5
print(heapArr.items) # [None, 1, 2, 43, 100, 3]
print(heapArr.extract()) # 1
print(heapArr.extract()) # 2'Algorithm' 카테고리의 다른 글
| [알고리즘/파이썬] 리트코드 leetcode 215. 배열의 K 번째 큰 요소 (1) | 2024.01.24 |
|---|

